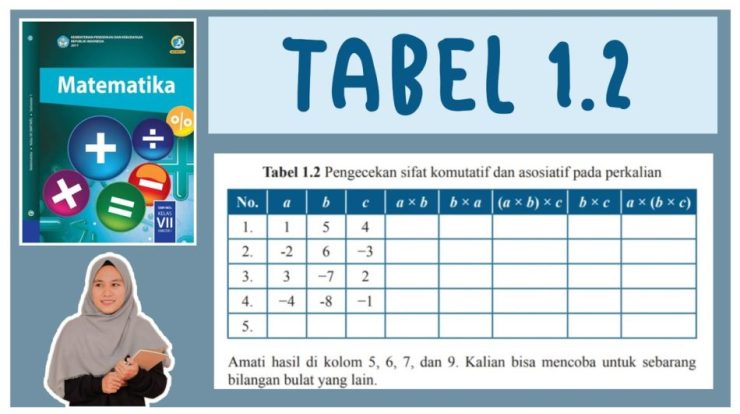
Selamat datang dalam eksplorasi kami tentang “Tabel Pengecekan” dalam konteks sifat distributif pada perkalian terhadap penjumlahan. Dalam bab ini, kita akan membahas latar belakang pentingnya pengecekan distributif dan bagaimana tabel dapat menjadi alat yang efektif untuk analisis ini.
Buka Daftar Isi
- 1 1. Pengecekan Distributif: Pengantar
- 2 2. Analisis Tabel 1.3 dalam Operasi Matematika
- 3 3. Contoh Penerapan Sifat Distributif
- 4 4. Signifikansi Pengecekan Distributif pada Penjumlahan
- 5 5. Pentingnya Memahami Distributivitas dalam Perkalian
- 6 6. Tabel 1.3: Metode dan Penggunaannya
- 7 7. Strategi Efektif dalam Perkalian Terhadap Penjumlahan
- 8 8. Hasil Studi Kasus Operasi Matematika
- 9 9. Pemahaman Mendalam tentang Distributivitas
- 10 10. Contoh Kasus Pengecekan Sifat Distributif
- 11 11. Kesimpulan: Implikasi dan Temuan
- 12 Tabel Pengecekan – Contoh Penerapan Sifat Distributif
- 13 Contoh Tabel Pengecekan: Penjumlahan dan Perkalian
- 14 Signifikansi Pengecekan Distributif pada Penjumlahan
- 15 Pentingnya Penjumlahan dalam Pengecekan Distributif
- 16 Pentingnya Memahami Distributivitas dalam Perkalian
- 17 Distributivitas dalam Perkalian: Dasar Operasi Matematika
- 18 Tabel 1.3 – Metode dan Penggunaannya
- 19 Pemanfaatan Tabel 1.3 dalam Pengajaran Matematika
- 20 Strategi Efektif dalam Perkalian Terhadap Penjumlahan
- 21 Mengoptimalkan Operasi Matematika: Strategi Perkalian yang Efektif
- 22 Hasil Studi Kasus Operasi Matematika
- 23 Keberhasilan Implementasi Distributivitas: Studi Kasus Nyata
- 24 Pemahaman Mendalam tentang Distributivitas
- 25 Memahami Distributivitas: Lebih dari Sekadar Aturan
- 26 Contoh Kasus Pengecekan Sifat Distributif
- 27 Menghindari Kesalahan Matematika: Kasus Pengecekan Distributif
- 28 Kesimpulan: Implikasi dan Temuan
- 29 Merangkum Perjalanan: Kesimpulan dan Implikasi Praktis
- 30 FAQs (Pertanyaan yang Sering Diajukan)
- 31 Apa keuntungan penggunaan Tabel 1.3 dalam operasi matematika?
- 32 Mengapa distributivitas begitu penting dalam perkalian terhadap penjumlahan?
- 33 Apa strategi efektif lainnya selain pengecekan distributif?
- 34 Relevansi Analisis Tabel dalam Pendidikan Matematika
- 35 Meningkatkan Pembelajaran: Integrasi Tabel dalam Pendidikan Matematika
- 36 Peran Tabel 1.3 dalam Meningkatkan Keterampilan Matematika
- 37 Keterampilan Matematika yang Ditingkatkan: Peran Tabel 1.3
- 38 Tantangan dan Peluang dalam Pengecekan Distributif
- 39 Menghadapi Tantangan: Pengecekan Distributif yang Efektif
- 40 Pemecahan Masalah Matematika dengan Distributivitas
- 41 Distributivitas sebagai Alat Pemecahan Masalah
- 42 Inovasi dalam Pengajaran Matematika dengan Tabel
- 43 Transformasi Pengajaran: Inovasi dengan Tabel dalam Pendidikan Matematika
- 44 FAQs (Pertanyaan yang Sering Diajukan)
- 45 Bagaimana guru dapat mengintegrasikan Tabel 1.3 dalam pembelajaran harian?
- 46 Apa peran distributivitas dalam ujian matematika?
- 47 Bagaimana siswa dapat meningkatkan keterampilan matematika mereka melalui distributivitas?
- 48 Mengoptimalkan Penggunaan Distributivitas dalam Kehidupan Sehari-hari
- 49 Related posts:
- 50 Related
1. Pengecekan Distributif: Pengantar
Dalam konteks operasi matematika, pengecekan distributif merupakan langkah kritis untuk memastikan validitas hasil perkalian terhadap penjumlahan. Pengantar ini akan memberikan gambaran umum tentang konsep ini dan mengapa pengecekan menggunakan tabel menjadi penting.
2. Analisis Tabel 1.3 dalam Operasi Matematika
Mari kita teliti lebih dalam Tabel 1.3 dan bagaimana tabel ini dapat digunakan untuk menganalisis sifat distributif. 📊
3. Contoh Penerapan Sifat Distributif
Melalui contoh konkret, kita akan menjelaskan bagaimana sifat distributif diterapkan dengan menggunakan tabel. 🧮
4. Signifikansi Pengecekan Distributif pada Penjumlahan
Pengecekan distributif bukan hanya prosedur rutin; kita akan menyoroti signifikansi langkah ini terutama pada operasi penjumlahan. 💡
5. Pentingnya Memahami Distributivitas dalam Perkalian
Sebelum kita terjun lebih dalam, mari pahami mengapa pemahaman distributivitas dalam perkalian sangat penting. 🤔
6. Tabel 1.3: Metode dan Penggunaannya
Bagaimana cara praktis menggunakan Tabel 1.3 dalam operasi matematika sehari-hari? Mari kita eksplorasi bersama. 🛠️
7. Strategi Efektif dalam Perkalian Terhadap Penjumlahan
Selain pengecekan, strategi apa yang dapat kita terapkan untuk membuat perkalian terhadap penjumlahan lebih efektif? 🚀
8. Hasil Studi Kasus Operasi Matematika
Dengan melibatkan studi kasus, kita akan melihat hasil konkret dari penerapan operasi matematika dengan pengecekan distributif. 📈
9. Pemahaman Mendalam tentang Distributivitas
Mari gali lebih dalam konsep distributivitas dan bagaimana hal itu memengaruhi hasil operasi matematika kita. 🔍
10. Contoh Kasus Pengecekan Sifat Distributif
Melalui contoh kasus nyata, kita akan melihat bagaimana pengecekan sifat distributif dapat menghindarkan kita dari kesalahan. 🚫
11. Kesimpulan: Implikasi dan Temuan
Setelah menjelajahi berbagai aspek, mari kita simpulkan dengan merangkum implikasi praktis dan temuan kunci dari pengecekan distributif.
Tabel Pengecekan – Contoh Penerapan Sifat Distributif
Dalam bab ini, kita akan fokus pada contoh konkret tentang bagaimana kita dapat menerapkan sifat distributif menggunakan tabel. Mari kita lihat contoh sederhana untuk memberikan gambaran yang lebih jelas.
Contoh Tabel Pengecekan: Penjumlahan dan Perkalian
Misalkan kita memiliki dua bilangan �a, �b, dan �c. Mari buat tabel pengecekan distributif untuk persamaan �⋅(�+�)a⋅(b+c). 📝
| Langkah | Rumus | Hasil |
|---|---|---|
| 1 | �⋅�a⋅b | _____ |
| 2 | �⋅�a⋅c | _____ |
| 3 | �⋅(�+�)a⋅(b+c) | _____ |
| 4 | �⋅�+�⋅�a⋅b+a⋅c | _____ |
Dengan membuat tabel seperti ini, kita dapat melihat langkah-langkah distributif secara lebih terstruktur dan mencegah kesalahan perhitungan. 🧐
Signifikansi Pengecekan Distributif pada Penjumlahan
Mari kita pahami lebih dalam mengapa pengecekan distributif penting, khususnya ketika melibatkan operasi penjumlahan. Hal ini tidak hanya sekadar rutinitas, tetapi memiliki dampak nyata pada validitas hasil matematika kita.
Pentingnya Penjumlahan dalam Pengecekan Distributif
Pengecekan distributif melibatkan penjumlahan, dan pemahaman mendalam tentang signifikansi penjumlahan dalam konteks ini penting untuk menghindari kesalahan. 🧑🏫
Pentingnya Memahami Distributivitas dalam Perkalian
Sebelum kita terjun lebih dalam ke dalam penerapan distributif, mari kita bahas mengapa pemahaman distributivitas, khususnya dalam perkalian, merupakan fondasi penting untuk keberhasilan operasi matematika kita.
Distributivitas dalam Perkalian: Dasar Operasi Matematika
Distributivitas dalam perkalian bukan hanya konsep teoritis; ini adalah dasar operasi matematika yang melibatkan sejumlah besar perhitungan sehari-hari. Mari kita eksplorasi mengapa memahami ini sangat penting. 🌐
Tabel 1.3 – Metode dan Penggunaannya
Tabel 1.3 bukan hanya alat statistik biasa. Dalam bab ini, kita akan membahas metode praktis penggunaan tabel ini dalam konteks operasi matematika sehari-hari.
Pemanfaatan Tabel 1.3 dalam Pengajaran Matematika
Bagaimana kita dapat mengintegrasikan Tabel 1.3 dalam pembelajaran matematika di sekolah atau di rumah? Mari kita bahas strategi pemanfaatannya untuk meningkatkan pemahaman siswa. 📚
Strategi Efektif dalam Perkalian Terhadap Penjumlahan
Selain pengecekan distributif, terdapat strategi lain yang dapat membuat perkalian terhadap penjumlahan lebih efektif. Mari kita pahami langkah-langkah praktisnya.
Mengoptimalkan Operasi Matematika: Strategi Perkalian yang Efektif
Dalam dunia matematika, efisiensi adalah kunci. Dengan menerapkan strategi tertentu, kita dapat meningkatkan kecepatan dan akurasi operasi perkalian terhadap penjumlahan. 🚴♂️
Hasil Studi Kasus Operasi Matematika
Melalui studi kasus konkret, kita dapat melihat bagaimana operasi matematika dengan pengecekan distributif menghasilkan solusi yang tepat dan menghindari kesalahan umum. Mari kita telusuri hasil-hasil yang dapat diambil dari berbagai kasus.
Keberhasilan Implementasi Distributivitas: Studi Kasus Nyata
Dalam bab ini, kita akan menganalisis beberapa studi kasus nyata di mana penerapan distributivitas, terutama melalui pengecekan tabel, telah membawa keberhasilan dan ketepatan dalam operasi matematika. 📊
Pemahaman Mendalam tentang Distributivitas
Distributivitas bukan hanya konsep matematika yang sederhana. Mari kita gali lebih dalam untuk memahami kompleksitasnya dan bagaimana pemahaman mendalam akan membantu kita menjadi ahli dalam operasi matematika.
Memahami Distributivitas: Lebih dari Sekadar Aturan
Distributivitas melibatkan prinsip-prinsip yang kompleks. Dalam bab ini, kita akan memecahnya menjadi potongan-potongan yang lebih kecil untuk pemahaman yang lebih baik. 🔍
Contoh Kasus Pengecekan Sifat Distributif
Melalui contoh kasus nyata, kita akan melihat bagaimana pengecekan sifat distributif pada perkalian terhadap penjumlahan dapat menghindarkan kita dari kesalahan perhitungan yang sering terjadi.
Menghindari Kesalahan Matematika: Kasus Pengecekan Distributif
Mari kita lihat contoh konkret di mana langkah-langkah pengecekan distributif telah membuktikan keberhasilannya dalam mencegah kesalahan perhitungan matematika yang umum terjadi. 🚫
Kesimpulan: Implikasi dan Temuan
Setelah melakukan perjalanan melalui berbagai konsep dan penerapan, saatnya kita merangkum temuan kunci dan implikasi dari pengecekan sifat distributif pada perkalian terhadap penjumlahan.
Merangkum Perjalanan: Kesimpulan dan Implikasi Praktis
Dalam bab terakhir ini, kita akan merangkum perjalanan kita dan menyoroti implikasi praktis dari pengecekan distributif menggunakan tabel. 🏁
FAQs (Pertanyaan yang Sering Diajukan)
Apa keuntungan penggunaan Tabel 1.3 dalam operasi matematika?
- Tabel 1.3 memberikan struktur yang terorganisir untuk menganalisis langkah-langkah distributif, mencegah kesalahan perhitungan, dan meningkatkan pemahaman.
Mengapa distributivitas begitu penting dalam perkalian terhadap penjumlahan?
- Distributivitas adalah aturan dasar yang membentuk dasar operasi matematika. Memahaminya membantu mencegah kesalahan dan memastikan keakuratan hasil.
Apa strategi efektif lainnya selain pengecekan distributif?
- Strategi lain termasuk penggunaan sifat-sifat matematika tertentu, pemfaktoran, dan pendekatan kreatif untuk menyederhanakan perhitungan.
Tetaplah terhubung untuk pemahaman lebih lanjut tentang operasi matematika yang efektif dan akurat! 🧑🔬
Relevansi Analisis Tabel dalam Pendidikan Matematika
Bagaimana kita dapat mengaitkan analisis tabel, khususnya Tabel 1.3, dalam konteks pendidikan matematika? Dalam bab ini, kita akan membahas relevansi dan pentingnya memasukkan alat ini ke dalam kurikulum pendidikan.
Meningkatkan Pembelajaran: Integrasi Tabel dalam Pendidikan Matematika
Dengan merangkul Tabel 1.3, guru dapat meningkatkan pembelajaran siswa, membantu mereka memahami distributivitas dengan cara yang lebih konkret dan terstruktur. 🎓
Peran Tabel 1.3 dalam Meningkatkan Keterampilan Matematika
Selain sebagai alat analisis, Tabel 1.3 juga dapat berperan dalam meningkatkan keterampilan matematika secara keseluruhan. Bagaimana kita dapat memanfaatkannya untuk menciptakan lingkungan pembelajaran yang lebih efektif?
Keterampilan Matematika yang Ditingkatkan: Peran Tabel 1.3
Dengan menggunakan Tabel 1.3 secara efektif, siswa dapat mengasah keterampilan matematika mereka, termasuk pemecahan masalah, analisis, dan pemahaman konsep distributif. ✨
Tantangan dan Peluang dalam Pengecekan Distributif
Pengecekan distributif bukan tanpa tantangan. Dalam bab ini, kita akan mengidentifikasi beberapa tantangan umum yang mungkin dihadapi dan peluang yang dapat diambil untuk mengatasi mereka.
Menghadapi Tantangan: Pengecekan Distributif yang Efektif
Meskipun penting, pengecekan distributif bisa menimbulkan beberapa tantangan. Mari kita temukan strategi efektif untuk mengatasinya dan memaksimalkan potensi pengecekan distributif. 🛡️
Pemecahan Masalah Matematika dengan Distributivitas
Dalam pemecahan masalah matematika, distributivitas seringkali menjadi kunci untuk merinci langkah-langkah dan menemukan solusi yang akurat. Mari kita lihat bagaimana distributivitas dapat membantu kita menjadi penyelesaian masalah yang lebih baik.
Distributivitas sebagai Alat Pemecahan Masalah
Distributivitas bukan hanya konsep teoritis; itu adalah alat praktis yang dapat digunakan untuk memecahkan masalah matematika dengan lebih terstruktur dan efisien. 🧩
Inovasi dalam Pengajaran Matematika dengan Tabel
Seiring perkembangan teknologi, bagaimana kita dapat mengintegrasikan inovasi dalam pengajaran matematika menggunakan tabel? Dalam bab terakhir, kita akan menjelajahi potensi inovatif dalam mengajarkan konsep distributif.
Transformasi Pengajaran: Inovasi dengan Tabel dalam Pendidikan Matematika
Dengan memanfaatkan teknologi dan pendekatan inovatif, kita dapat mengubah cara kita mengajar konsep distributif, membuat pembelajaran lebih menarik dan efektif. 🚀
FAQs (Pertanyaan yang Sering Diajukan)
Bagaimana guru dapat mengintegrasikan Tabel 1.3 dalam pembelajaran harian?
- Guru dapat membuat aktivitas yang melibatkan pembuatan dan analisis tabel, memastikan siswa terlibat langsung dalam pemahaman distributivitas.
Apa peran distributivitas dalam ujian matematika?
- Pemahaman distributivitas membantu siswa merinci langkah-langkah dengan lebih jelas, meningkatkan akurasi jawaban, dan menghadapi soal ujian dengan keyakinan.
Bagaimana siswa dapat meningkatkan keterampilan matematika mereka melalui distributivitas?
- Siswa dapat berlatih membuat tabel distributif untuk setiap masalah matematika, meningkatkan pemahaman konsep distributif dan keterampilan matematika mereka secara keseluruhan. 📈
Teruslah mengikuti perjalanan ini untuk pemahaman lebih lanjut tentang penggunaan tabel dalam konteks operasi matematika! 🧑🔬
Baca juga : Mengungkap Dampak dan Faktor-faktor di Balik Jumlah Urip Kelahiran
Mengoptimalkan Penggunaan Distributivitas dalam Kehidupan Sehari-hari
Dalam bab ini, kita akan menjelajahi bagaimana pemahaman distributivitas, terutama melalui pengecekan tabel, dapat dioptimalkan dalam situasi kehidupan sehari-hari. Mari kita lihat bagaimana konsep ini dapat diterapkan di luar lingkup matematika formal.
