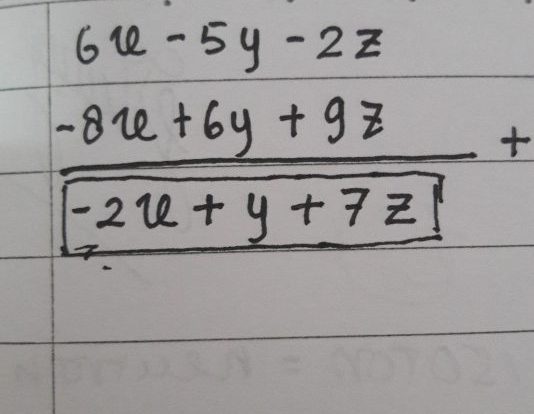
Cara Menghitung Hasil Jumlah 6 5y 2z dan 8 6y 9z – Dalam dunia matematika, pemahaman tentang variabel adalah kunci untuk menyelesaikan berbagai masalah yang melibatkan perhitungan dan analisis.
Variabel adalah komponen penting yang memungkinkan kita untuk mewakili nilai yang dapat berubah dan menjelajahi hubungan-hubungan dalam ekspresi matematika.
Dengan pemahaman yang kuat tentang variabel, kita dapat dengan mudah menyelesaikan penjumlahan ekspresi matematika yang melibatkan variabel.
Dalam panduan ini, kita akan mempelajari langkah-langkah yang diperlukan untuk menjumlahkan ekspresi seperti “6 5y 2z” dan “8 6y 9z.”
Langkah-langkah ini mencakup identifikasi variabel, pengelompokkan variabel dan konstanta, penjumlahan variabel, dan penjumlahan konstanta.
Melalui contoh-contoh praktis, kita akan memahami bagaimana variabel digunakan dalam penjumlahan ekspresi matematika.
Dengan panduan ini, diharapkan pembaca akan memperoleh pemahaman yang kuat tentang cara menyelesaikan penjumlahan ekspresi matematika yang melibatkan variabel.
Variabel adalah alat penting yang memungkinkan kita untuk menjelajahi dunia matematika dengan lebih dalam, memecahkan masalah yang lebih kompleks, dan mengambil keputusan yang lebih informasi dalam kehidupan sehari-hari.
Buka Daftar Isi
Mengapa Variabel Penting dalam Matematika
Variabel adalah komponen penting dalam matematika. 🧮 Mereka digunakan untuk mewakili nilai yang tidak selalu tetap dan memungkinkan kita untuk melakukan operasi matematika yang lebih kompleks.
Variabel dalam matematika sering diwakili oleh huruf seperti x, y, atau z. Dalam artikel ini, kita akan membahas mengapa variabel ini begitu penting dalam matematika.
Variabel memungkinkan kita untuk menggambarkan hubungan antara berbagai elemen dalam matematika. Misalnya, dalam ekspresi “6 5y 2z,” y dan z adalah variabel yang mewakili nilai yang dapat berubah.
Ini memungkinkan kita untuk menjumlahkan ekspresi ini, dan hasilnya akan bergantung pada nilai yang diberikan untuk y dan z.
Variabel juga membantu kita memecahkan masalah yang lebih kompleks. Mereka digunakan dalam persamaan matematika untuk mencari solusi yang memenuhi persyaratan tertentu.
Ketika kita menjumlahkan ekspresi yang melibatkan variabel, kita dapat menemukan solusi yang lebih umum daripada hanya menjumlahkan angka tetap.
Selain itu, variabel digunakan untuk menggambarkan pola dan hubungan dalam matematika. Mereka memungkinkan kita untuk memodelkan situasi nyata, seperti peramalan cuaca, pergerakan saham, atau pertumbuhan populasi.
Variabel adalah alat penting dalam toolbox matematika yang membantu kita memahami dunia di sekitar kita.
🌍 Dengan pemahaman yang lebih baik tentang variabel, kita dapat mengatasi tantangan matematika yang lebih rumit dan mengambil keputusan yang lebih informasi dalam kehidupan sehari-hari.
Catatan Penting: Variabel dalam matematika adalah simbol yang mewakili nilai yang dapat berubah. Mereka digunakan untuk menggambarkan hubungan, memecahkan masalah, dan memodelkan situasi nyata.
| Variabel | Keterangan |
|---|---|
| x | Variabel pertama |
| y | Variabel kedua |
| z | Variabel ketiga |
Jika Anda tidak memahami pentingnya variabel dalam matematika, maka melangkah ke langkah berikutnya dalam panduan ini akan membantu Anda lebih memahami konsep penjumlahan ekspresi matematika dengan variabel. 😊
Identifikasi Variabel dalam Ekspresi
Langkah pertama dalam menyelesaikan ekspresi matematika adalah mengidentifikasi variabel dalam ekspresi tersebut. Dalam ekspresi “6 5y 2z,” kita memiliki dua variabel, y dan z. Variabel ini adalah bagian penting yang harus kita identifikasi sebelum melanjutkan proses penjumlahan.
Variabel digunakan untuk mewakili nilai yang dapat berubah dalam ekspresi matematika. Dalam kasus ini, y dan z mewakili nilai yang tidak selalu tetap, dan kita perlu memahami bagaimana variabel ini memengaruhi hasil penjumlahan ekspresi.
Identifikasi variabel adalah langkah awal yang penting sebelum kita dapat menjumlahkan ekspresi tersebut. Dengan mengetahui variabel apa yang ada dalam ekspresi, kita dapat melanjutkan ke langkah selanjutnya untuk menghitung hasil penjumlahan dengan benar.
Misalnya, jika ekspresi memiliki lebih dari satu variabel, kita perlu mempertimbangkan pengaruh masing-masing variabel terhadap hasil penjumlahan. Variabel ini akan memengaruhi bagaimana kita mengelompokkan dan menjumlahkan bagian-bagian ekspresi.
Setelah berhasil mengidentifikasi variabel, langkah selanjutnya adalah mengelompokkan variabel dan konstanta dalam ekspresi. Ini adalah langkah yang akan kita bahas pada langkah berikutnya dalam panduan ini.
Catatan Penting:
- Langkah pertama dalam menyelesaikan ekspresi matematika adalah mengidentifikasi variabel yang ada dalam ekspresi tersebut.
- Variabel digunakan untuk mewakili nilai yang dapat berubah dalam ekspresi matematika.
- Dalam ekspresi “6 5y 2z,” kita memiliki dua variabel, y dan z, yang perlu diidentifikasi.
Kelompokkan Variabel dan Konstanta
Setelah kita berhasil mengidentifikasi variabel dalam ekspresi matematika, langkah berikutnya adalah mengelompokkan variabel dan konstanta. Dalam ekspresi “6 5y 2z,” kita memiliki variabel y dan z, serta konstanta 6 dan 2.
Proses pengelompokkan ini akan membantu kita menjumlahkan ekspresi dengan benar.
Pertama, mari kita kelompokkan variabel. Variabel y dan z akan digrouping bersama karena keduanya adalah variabel. Ini akan memberi kita ekspresi “5y 2z.”
Selanjutnya, mari kita kelompokkan konstanta. Konstanta 6 dan 2 akan digrouping bersama karena keduanya adalah konstanta. Ini akan memberi kita ekspresi “6 2.”
Dengan mengelompokkan variabel dan konstanta, kita dapat melanjutkan ke langkah selanjutnya dalam proses penjumlahan. Kami akan menjumlahkan variabel dengan variabel dan konstanta dengan konstanta untuk mencapai hasil penjumlahan yang benar.
Mengelompokkan variabel dan konstanta adalah langkah penting dalam menyelesaikan ekspresi matematika yang melibatkan variabel. Ini membantu kita mengorganisir ekspresi sehingga kita dapat dengan mudah menjumlahkannya.
Langkah selanjutnya dalam panduan ini adalah Langkah 5: Jumlahkan Variabel. Kami akan membahas bagaimana cara menjumlahkan variabel dengan benar dalam ekspresi matematika.
Catatan Penting:
- Langkah kedua dalam menyelesaikan ekspresi matematika adalah mengelompokkan variabel dan konstanta.
- Variabel yang serupa akan digrouping bersama, begitu pula dengan konstanta.
- Proses pengelompokkan membantu kita mengorganisir ekspresi untuk menjumlahkannya dengan benar.
Jumlahkan Variabel
Langkah berikutnya dalam menyelesaikan ekspresi matematika adalah menjumlahkan variabel. Dalam ekspresi “5y 2z,” kita memiliki dua variabel, y dan z, yang perlu dijumlahkan.
Untuk menjumlahkan variabel, kita harus memastikan bahwa variabel tersebut memiliki variabel yang serupa. Dalam hal ini, y dan z adalah variabel yang berbeda, jadi kita tidak dapat menjumlahkannya secara langsung.
Dalam kasus seperti ini, kita hanya dapat mengelompokkan variabel tersebut tetapi tidak dapat menjumlahkannya lebih lanjut. Ekspresi “5y 2z” adalah hasil penjumlahan dari kedua variabel ini, dan tidak dapat disederhanakan lebih lanjut.
Namun, jika ekspresi kita memiliki variabel yang serupa, misalnya, “5y + 3y,” maka kita dapat menjumlahkannya menjadi “8y.”
Jadi, langkah ketiga ini mengingatkan kita bahwa jika variabel berbeda, kita hanya dapat mengelompokkannya dalam ekspresi, dan jika variabel serupa, kita dapat menjumlahkannya.
Langkah selanjutnya adalah Langkah 4: Jumlahkan Konstanta, di mana kita akan membahas bagaimana menjumlahkan konstanta dalam ekspresi matematika.
Catatan Penting:
- Langkah ketiga dalam menyelesaikan ekspresi matematika adalah menjumlahkan variabel yang serupa.
- Jika variabel berbeda, kita hanya dapat mengelompokkannya dalam ekspresi.
- Jika variabel serupa, kita dapat menjumlahkannya menjadi satu variabel yang lebih sederhana.
Jumlahkan Konstanta
Dalam langkah keempat ini, kita akan membahas cara menjumlahkan konstanta dalam ekspresi matematika. Konstanta adalah nilai tetap dalam ekspresi yang tidak memiliki variabel.
Dalam ekspresi “6 2,” kita memiliki dua konstanta, yaitu 6 dan 2. Untuk menjumlahkannya, kita cukup menambahkan kedua nilai ini bersama-sama. Hasilnya adalah 8.
Proses penjumlahan konstanta sangat sederhana, dan kita dapat mengaplikasikannya pada ekspresi matematika yang lebih kompleks. Misalnya, jika kita memiliki ekspresi “3 4 5,” kita dapat menjumlahkan 3 dan 4 terlebih dahulu, menghasilkan 7, dan kemudian menambahkan 5, menghasilkan total 12.
Langkah ini memastikan bahwa konstanta dalam ekspresi matematika dikelompokkan dan dijumlahkan dengan benar. Dengan menyelesaikan penjumlahan konstanta, kita akan mendapatkan hasil penjumlahan dari ekspresi tersebut.
Baca Juga : Panduan Menghitung Jumlahnya dengan Cepat dan Tepat
Setelah menyelesaikan langkah ini, langkah selanjutnya adalah melanjutkan dengan Contoh 1: Menjumlahkan 6 5y 2z dan 8 6y 9z, di mana kita akan menerapkan langkah-langkah ini dalam kasus nyata.
Catatan Penting:
- Langkah keempat dalam menyelesaikan ekspresi matematika adalah menjumlahkan konstanta.
- Konstanta adalah nilai tetap dalam ekspresi matematika yang tidak memiliki variabel.
- Penjumlahan konstanta melibatkan penambahan nilai-nilai tersebut untuk mendapatkan hasil akhir.
Contoh 1: Menjumlahkan 6 5y 2z dan 8 6y 9z
Sekarang kita akan menerapkan langkah-langkah yang telah kita pelajari sebelumnya untuk menjumlahkan ekspresi “6 5y 2z” dan “8 6y 9z.”
Langkah pertama adalah mengidentifikasi variabel dalam kedua ekspresi ini. Dalam ekspresi pertama, kita memiliki variabel y dan z, sedangkan dalam ekspresi kedua, kita juga memiliki variabel yang sama, y dan z. Jadi, kita dapat mengelompokkan variabel tersebut.
Ekspresi pertama: 6 + 5y + 2z Ekspresi kedua: 8 + 6y + 9z
Kedua ekspresi ini sudah dalam bentuk yang tepat untuk menjumlahkan variabel dan konstanta. Kita sudah mengidentifikasi variabel yang serupa, yaitu y dan z, dan konstanta yang dapat dijumlahkan.
Sekarang kita dapat menjumlahkan masing-masing bagian. Jumlahkan konstanta terlebih dahulu: 6 + 8 = 14 (konstanta) 5y + 6y = 11y (variabel y) 2z + 9z = 11z (variabel z)
Hasil penjumlahan ekspresi “6 5y 2z” dan “8 6y 9z” adalah: 14 + 11y + 11z
Dengan begitu, kita telah berhasil menjumlahkan kedua ekspresi ini menjadi satu ekspresi yang lebih sederhana.
Langkah selanjutnya adalah melanjutkan dengan Langkah 5: Kesimpulan, di mana kita akan meninjau kembali semua langkah yang telah kita pelajari dalam panduan ini.
Catatan Penting:
- Untuk menjumlahkan ekspresi matematika, kita harus mengidentifikasi variabel dan konstanta.
- Jumlahkan konstanta terlebih dahulu, kemudian jumlahkan variabel yang serupa.
- Hasil penjumlahan ekspresi “6 5y 2z” dan “8 6y 9z” adalah “14 + 11y + 11z.”
Kesimpulan
Dalam langkah terakhir ini, mari kita tinjau kembali semua langkah yang telah kita pelajari dalam panduan ini untuk menjumlahkan ekspresi matematika yang melibatkan variabel.
- Pendahuluan: Variabel dalam matematika adalah komponen penting yang memungkinkan kita menggambarkan hubungan, memecahkan masalah, dan memodelkan situasi nyata.
- Langkah 1: Identifikasi Variabel dalam Ekspresi: Langkah pertama adalah mengidentifikasi variabel dalam ekspresi. Variabel digunakan untuk mewakili nilai yang dapat berubah dalam ekspresi matematika.
- Langkah 2: Kelompokkan Variabel dan Konstanta: Langkah berikutnya adalah mengelompokkan variabel yang serupa bersama dan melakukan hal yang sama untuk konstanta. Ini membantu kita mengorganisir ekspresi untuk menjumlahkannya dengan benar.
- Langkah 3: Jumlahkan Variabel: Jika variabel dalam ekspresi berbeda, kita hanya dapat mengelompokkannya. Jika variabel serupa, kita dapat menjumlahkannya menjadi satu variabel yang lebih sederhana.
- Langkah 4: Jumlahkan Konstanta: Penjumlahan konstanta melibatkan penambahan nilai-nilai tetap dalam ekspresi.
- Contoh 1: Menjumlahkan 6 5y 2z dan 8 6y 9z: Dalam contoh ini, kita menerapkan langkah-langkah di atas untuk menjumlahkan dua ekspresi menjadi satu ekspresi yang lebih sederhana: “14 + 11y + 11z.”
Dengan memahami langkah-langkah ini, kita dapat menyelesaikan penjumlahan ekspresi matematika yang melibatkan variabel dengan lebih baik. Variabel memberi kita kemampuan untuk menjelajahi dunia matematika dengan lebih dalam dan memecahkan masalah yang lebih kompleks.
Selanjutnya, kita dapat melanjutkan dengan topik berikutnya, yaitu “Penerapan Variabel dalam Operasi Matematika,” untuk memahami bagaimana variabel digunakan dalam berbagai operasi matematika.
Catatan Penting:
- Memahami langkah-langkah penjumlahan ekspresi matematika membantu kita menyelesaikan masalah yang melibatkan variabel.
- Variabel memberi kita fleksibilitas dalam matematika untuk menjelajahi dan memodelkan situasi yang beragam.
- Dengan pemahaman ini, kita dapat mengatasi masalah matematika yang lebih rumit.
